■フィボナッチとは
フィボナッチ Fibonacci 1170ころ‐1240以後
キリスト教的ヨーロッパ世界が生んだ最初の偉大な数学者。レオナルド・ダ・ピサ Leonardo daPisa,レオナルド・ピサーノ Leonardo Pisano ともいう。
地中海地域の商業活動に携わるかたわら,高度に発達したアラビア数学の技法を身につけ,後世に大きな影響を与える著作を書いた。
その名声は,時の神聖ローマ帝国皇帝フリードリヒ2世にも届き,晩年にはピサ共和国から〈卓越し学識あるレオナルド〉の名を与えられ,年金を供与されたことが記録に残されている。
主著《アバクスの書Liber abaci》(別称《算術の書》。1202,1228改訂)は,インド・アラビア式数字(今日の算用数字)による筆算法をヨーロッパ世界に伝えた画期的な書物である。その最終章は,フワーリズミーやアブー・カーミルの二次方程式論を取り扱っている。アラビアの代数学を伝えた点で,彼はヨーロッパ後期中世の商業用代数学(コス式技法)の祖とみなされる。
(以上 平凡社『世界大百科事典』より)
■フィボナッチ数とは
漸化式 U0=0,U1=1,……,Un=U(n-1)+U(n-2) (n=2,3,4,……)
で定義される数列{Un}をフィボナッチ数列,
各項をフィボナッチ数といいます。
初項から並べると、
1, 1, 2, 3, 5,8, 13, 21, 34, 55, 89,144, 233,......となります。
この数列は、テクニカル分析において非常に重要な数値として扱われ、
西欧のトレーダーはテクニカル分析でこの数値をパラメーターとして利用することが多いと言われています。
■フィボナッチ数の特徴
(1)どの数字も上位の数字に対して0.618:1近づいていく。
1÷2=0.5
5÷8=0.625
21÷34≒0.6176
89÷144≒0.618
(2)どの数字も2つ上位の数字に対して0.382:1に近づいていく。
8÷21≒0.381
13÷34≒0.382
21÷55≒0.382
(3)どの数字も3つ上位の数字に対して0.236:1に近づいていく。
8÷34≒0.235
13÷55≒0.236
21÷89≒0.236
上記の比率(0.618)は古代ギリシャやエジプトで
黄金比率、黄金分割などと呼ばれていたもので、
美術、 建築などに応用されています。
■フィボナッチリトレースメントとは
上記のフィボナッチ数間の比0.236, 0.382, 0.5, 0.618,を用いて、
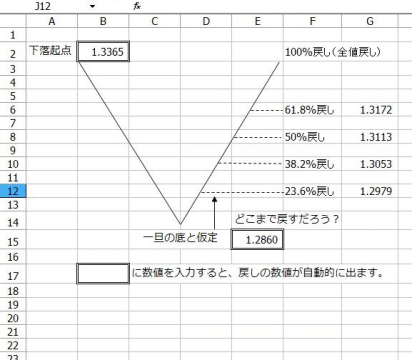
相場の押しや戻りの目標価格を推測する手法として、フィボナッチリトレースメントが使われます。
■計算ツール
フィボナッチリトレースメントを簡単にできる表をエクセルで作ってみました。
ダウンロードしてお使いください。
わざわざエクセルで計算しなくても、チャートソフトの
・DealBook FX(取り扱い:DRAGON FX
,AFT
)、
・Saxo(取り扱い:JNS
)
でも標準で利用できます。
※外為どっとコムのDreamVisorでは利用できないようです。
■例
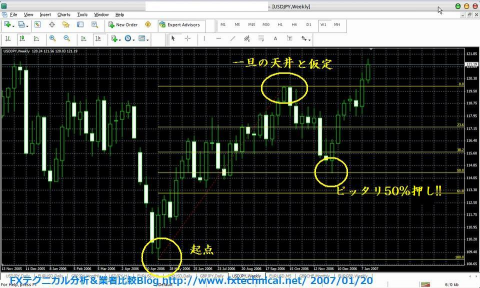
■ドル円2006年週足
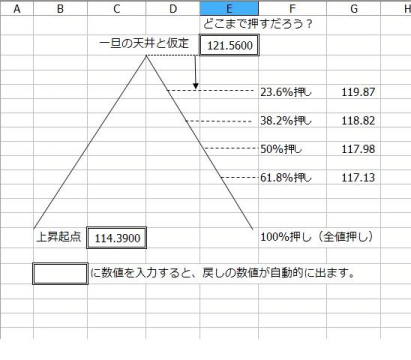
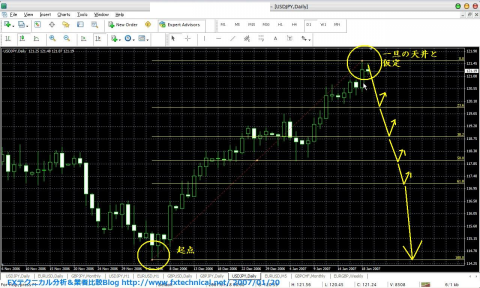
■ドル円114.39→121.56を一旦の天井と仮定した場合の押し目予想
以上、ご参考になれば幸いです。