先ほど、メルマガ最新号
FX・株のテクニカル分析入門 第536号
エリオット波動論再入門 148 フィボナッチ級数 7 φ(ファイ)の意味
を発行致しました。
以下は前号のバックナンバーです。
FX・株のテクニカル分析入門 第535号 エリオット波動論再入門 147 フィボナッチ級数 6 黄金らせん、対数螺旋(ロガリズミック・スパイラル)
━━━[お知らせ ]━━━━━━━━━━━━━━━━━━
今月のキャンペーン一覧
http://hikaku.fxtec.info/fxfxfx.html
━━━━━━━━━━━━━━━━━━━━━━━━━━━━
こんばんは。
FXTECです。
いつもご愛読ありがとうございます。
感謝します。
さて、本日は、
エリオット波動論再入門 147 フィボナッチ級数 6 黄金らせん、対数螺旋(ロガリズミック・スパイラル)
をご紹介いたします。
http://fxtechnicalblog.fxtec.info/imgs/fibonacci.jpg

http://fxtechnicalblog.fxtec.info/img2017/618.jpg
http://fxtechnicalblog.fxtec.info/img2017/ougon.png
http://fxtechnicalblog.fxtec.info/img2017/GoldenRectangle.jpg
http://fxtechnicalblog.fxtec.info/imgs/logarithmicspiral.jpg

http://en.wikipedia.org/wiki/Image:NautilusCutawayLogarithmicSpiral.jpg

http://en.wikipedia.org/wiki/Image:Low_pressure_system_over_Iceland.jpg

http://en.wikipedia.org/wiki/Image:Messier51.jpg

※日経平均CFDを売買できるFX会社・証券会社
DMM.com証券、手数料無料、日経CFDスプレッド7、レバレッジ10倍
http://fxtechnicalblog.fxtec.info/url/r.cgi?dmm-cfd
GMOクリック証券、手数料無料、日経CFDスプレッド2~9変動、レバレッジ10倍
http://fxtechnicalblog.fxtec.info/url/r.cgi?gmo-cfd
IG証券、手数料無料、日経CFDスプレッド8、レバレッジ10倍
http://fxtechnicalblog.fxtec.info/url/r.cgi?ig-shoken-cfd
■はいはい、で、エリオットって何だっけ?
エリオットとは、
米国の伝説のテクニカルアナリスト
Ralph Nelson Elliott ラルフ・ネルソン・エリオット(1871~1948)
http://fxtechnicalblog.fxtec.info/imgs/Elliot.gif

のことです。
一見して真面目そうな方です。
エリオットはレストランと鉄道を専門とする会計士で、
メキシコや中央アメリカの鉄道会社、政府機関などを転々とした後、
重病に罹り、58歳で退職。
その後数年間、カリフォルニアの自宅で療養生活を送りますが、
その間に、株式市場に関する独自の理論を構築したと言われています。
その後1938年(第二次世界大戦直前)、
エリオットが書いた論文をまとめた
「The Wave Principle(エリオット波動原理)」
(Charles J. Collinsとの共著)
が出版されました。
現在広く知られているエリオット波動理論は、
この「The Wave Principle」に基づいています。
■はいはい、で、ピサのレオナルド・フィボナッチって何やねん?
http://fxtechnicalblog.fxtec.info/imgs/fibonacci.jpg

「レオナルド・フィボナッチは、優れた商人であり、
また市の役人の息子として1170~1180年に生まれ、
ピサにある多くの塔のひとつに住んでいたと思われる。
(中略)
レオナルドはすでに学生時代に、
商売用の計算機としてヨーロッパで広く使われていた算盤の使い方を含めて、
税関や当時の商売の実務にも精通していた。
彼の母国語はイタリア語だったが、フランス語やギリシャ語、
さらにはラテン語も含む数カ国語を学び、
それらを流ちょうに話すことができた。
(中略)
レオナルドは有名な『算盤の書(Liber Abaci)』を出版した。
この本は世紀の偉大な数学的発見のひとつ、
いわゆる記数法の最初の数字として0を置く10進法を
ヨーロッパに紹介することになった。
0、1、2、3、4、5、6、7、8、9という親しみのある記号を含むこの方式は、
現在世界中で使用されているヒンズー・アラビア方式として知られている。
(中略)
そして彼の尽力によって、
やさしい計算法であるこの新しい方式は
最終的にヨーロッパに伝えられた。
その結果、従来のローマ数字は
次第にアラビア数字の体系に取って代わられていった。
この新しい方式のヨーロッパへの導入は、
700年以上も前にローマが滅亡して以来、
数学分野における最初の偉業であった。
フィボナッチは中世時代を通じて数学を生かし続けただけでなく、
いっそう高度な数学の分野と
物理学・天文学・技術工学などの関連分野においても、
偉大な発展の基礎を築いた。」
以上、『エリオット波動入門』より引用
http://fxtechnicalblog.fxtec.info/url/r.cgi?elliot2014
《コメント》
要は、アラビア数字の計算システムをヨーロッパに伝えた人、ということです。
詳しくはwikipediaも御覧ください。
■はいはい、で、黄金らせんって何やねん?
http://fxtechnicalblog.fxtec.info/img2017/GoldenRectangle.jpg

http://fxtechnicalblog.fxtec.info/imgs/logarithmicspiral.jpg

http://en.wikipedia.org/wiki/Image:NautilusCutawayLogarithmicSpiral.jpg

http://en.wikipedia.org/wiki/Image:Low_pressure_system_over_Iceland.jpg

http://en.wikipedia.org/wiki/Image:Messier51.jpg

http://fxtechnicalblog.fxtec.info/img2017/ougon.png
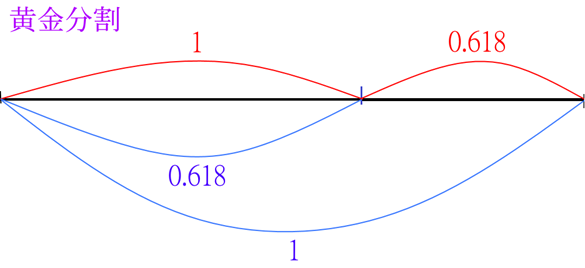
「黄金長方形を使えば、黄金らせんを作ることができる。
図3.5に示したような黄金長方形を正方形に分割していくと、
黄金長方形はどんどん小さくなっていく(図3.6を参照)。
(中略)
らせんは動き(すなわち、成長と衰退、拡大と収縮、進歩と退歩など)を示唆する。
対数らせんは宇宙全体で見られる自然の成長の現象を
本質的に表している。
それは、小は原子粒子の動きから、
大は銀河系に至るすべての大きさを内包している。
(中略)
彗星の尾は太陽から対数らせんを描きながら遠ざかっていく。
クモは対数らせん状にクモの巣を作る。
バクテリアは対数らせん状に点を結ぶような速度で増殖していく。
(中略)
ありとあらゆるものが対数らせん形をしている。
(中略)
おそらく基本的な法則である1.618という比率が、
自然のダイナミックな現象を支配しているのであろう。
このように、黄金らせんは自然界の壮大な形のひとつとして、
終わりのない拡大と縮小の力として、
そしてダイナミックなプロセスを支配する不変の法則として、
象徴的な形をとってわれわれの目の前に広がっている。
それらすべての根底にあるのは、
中庸としての1.618の比率である。」
http://fxtechnicalblog.fxtec.info/img2017/GoldenRectangle.jpg

http://fxtechnicalblog.fxtec.info/imgs/logarithmicspiral.jpg

http://en.wikipedia.org/wiki/Image:NautilusCutawayLogarithmicSpiral.jpg

http://en.wikipedia.org/wiki/Image:Low_pressure_system_over_Iceland.jpg

http://en.wikipedia.org/wiki/Image:Messier51.jpg


http://fxtechnicalblog.fxtec.info/img2017/ougon.png
以上、『エリオット波動入門』より引用
http://fxtechnicalblog.fxtec.info/url/r.cgi?elliot2014
《コメント》
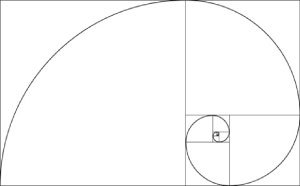
黄金らせん golden spiral とは、
黄金比 φ に関連した対数螺旋(ロガリズミック・スパイラル)の一種です。
http://fxtechnicalblog.fxtec.info/img2017/GoldenRectangle.jpg
詳しく知りたい方は、wikipediaをご参照ください。
黄金螺旋 - Wikipedia
https://goo.gl/JMqyWN
対数螺旋 - Wikipedia
https://goo.gl/26ioMH
画像検索して画像を眺めてみると結構面白いです。
黄金螺旋 https://goo.gl/RUDuRC
対数螺旋 https://goo.gl/bNca4q
なお、チャートにつきまして、
エリオット波動理論では終値を重視します。
この点、為替の日足分析で注意すべき点として、
為替は24時間地球上のどこかで取引が可能なため、
本質的に日足の始値、終値という概念がありません。
そこで便宜上、世界の金融センター、ニューヨークの終値を
日足の終値にするのが良いとされています。
この点、
FXプライム byGMO
http://fxtechnicalblog.fxtec.info/url/r.cgi?prime
DMM.com証券
http://fxtechnicalblog.fxtec.info/url/r.cgi?dmmfx
みんなのFX
http://fxtechnicalblog.fxtec.info/url/r.cgi?pan
マネーパートナーズ
http://fxtechnicalblog.fxtec.info/url/r.cgi?4
(以上、すべて無料で使えます)
などは、日足の終値がニューヨーク終値なので
ローソク足確認用におすすめです。
以上、少しでもご参考になりましたら幸いです。
■テクニカル分析ツール
テクニカル指標を表示するには、以下のツールを使うと便利です。
それぞれに利点があるので、
以下の5つを用途によって使い分けるのがいいと思います。
いずれも無料なので、いざというときの為にも、
5つともいつでも使える状態にすることをおすすめします。
※FXチャートソフト比較特集
チャート画面の画像付きで各社のチャートを徹底比較しています。
http://fxtechnicalblog.fxtec.info/fx_9/fx_13/
【1】 ぱっと見テクニカル
FXプライム byGMO のぱっと見テクニカルは、チャートフォーメーションや
テクニカル売買サインを自動で計算して通知してくれるので
とても便利です。正確な一目均衡表の表示ももちろん可能。
日足の区切りはNYクローズ採用。
→ http://fxtechnicalblog.fxtec.info/url/r.cgi?prime 【無料】
フォーメーション分析入門
http://fxtechnicalblog.fxtec.info/fx_9/cat128/
【2】 みんなのFX、外為ジャパン(旧MJ) (初心者から上級者まで)
正確な一目均衡表の表示が可能です。
チャート上にニュース、重要指標の結果等を表示できるので便利です。
日足の区切りはNYクローズ採用。
みんなのFX 【無料】
→ http://fxtechnicalblog.fxtec.info/url/r.cgi?pan
外為ジャパン(旧MJ) 【無料】
→ http://fxtechnicalblog.fxtec.info/url/r.cgi?1192
【3】 マネーパートナーズ ハイパースピード(初心者から上級者まで)
正確な一目均衡表の表示が可能です。
多数のテクニカル指標を利用可能。
日足の区切りはNYクローズ採用。
→ http://fxtechnicalblog.fxtec.info/url/r.cgi?4 【無料】
【4】GMOクリック証券Platinum Chart
Webブラウザで利用するチャートですが、非常に高機能。
正確な一目均衡表の表示が可能です。
日足の区切りはNYクローズ採用。
→ http://fxtechnicalblog.fxtec.info/url/r.cgi?csec 【無料】
【5】 MetaTrader 4(中級以上向け)
日足の区切りは各業者でバラバラです。
日足で利用するには色々と知識が必要です。
→MetaTraderまとめWiki http://hikaku.fxtec.info/metatrader/
その他、業者比較はこちらで。
http://hikaku.fxtec.info/
■ 次回予告
次回は、
エリオット波動論再入門 148 フィボナッチ級数 7 ファイの意味
をご紹介いたします。
───────────────────────────────────
発行者サイト
FXテクニカル分析&業者比較Blog
http://fxtechnicalblog.fxtec.info/
外為FX業者比較完全データベース
http://hikaku.fxtec.info/
お問い合わせ: fx@fxtechnical.net
メルマガバックナンバー
http://fxtechnicalblog.fxtec.info/fx_9/fx_6/
当メルマガにかかわるすべての権利は当メルマガの発行者が有しています。
許可なく転載、複製、販売、放送、レンタルすること、及びオークションへ
の出品・販売等は、法律により禁止されています。
───────────────────────────────────